Willem Hoek
Jane Street puzzle Feb 2021 SOLVED! OCaml to the rescue
Mar 08, 2021

Angler on a Wintry Lake, Ma Yuan, 1195
Hooks #7
Another month, another fun puzzle from Jane Street.
The grid below can be partitioned into 9 L-shaped “hooks”. The largest is 9-by-9 (contains 17 squares), the next largest is 8-by-8 (contains 15 squares), and so on. The smallest hook is just a single square. Find where the hooks are located, and place nine 9’s in the largest hook, eight 8’s in the next-largest, etc., down to one 1 in the smallest hook.
The filled squares must form a connected region. (Squares are “connected” if they are orthogonally adjacent.) Furthermore, every 2-by-2 region must contain at least one unfilled square.
The sum of the values in each of the connected shaded regions must be the same (there are 19 such regions).
The answer to this puzzle is the product of the areas of the connected groups of empty squares in the completed grid.
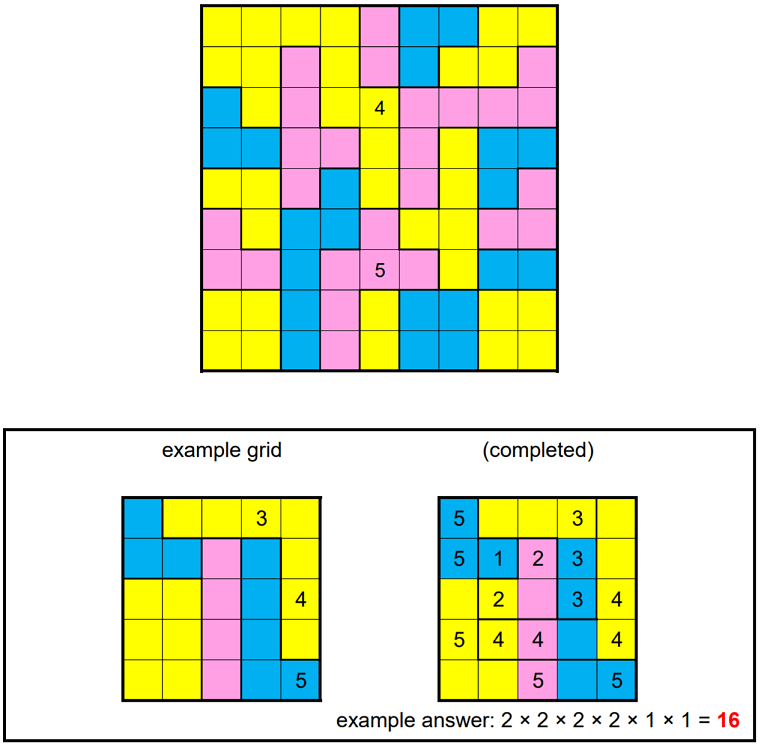
Approach followed
I began the puzzle in week 2 of the month and there were already 60+ people on the leader-board! This is more that most months, so I suspected this puzzle would be quite easy.
To get my algorithm / programming skills up I decided to solve this programmatically rather than with pen and paper. In short - the approach was, find all hook placement combinations (or grids) that satisfy the basic constraints and then use recursive backtracking to try to solve the grids fully.
Step 1. Determine how many unique placements of hooks are possible
There are 8 L-shaped pieces or hooks and one square that needs to be placed on the grid. The hooks can be placed in one of 4 positions, so that makes it 4^8 = 65,536 possible grid combinations.
function full_grid : string -> int array array
Using the example from the Jane Street website: full_grid "0323"
5 3 3 3 4 where 0 -> hook corner in BOTTOM LEFT
5 1 2 3 4 1 -> hook corner in TOP LEFT
5 2 2 3 4 2 -> hook corner in TOP RIGHT
5 4 4 4 4 3 -> hook corner in BOTTOM RIGHT
5 5 5 5 5
Step 2. Reduce the number of valid grid positions
There are 19 coloured regions on the grid. Every region must have the same total. That means that numbers in every region must add up to 15.
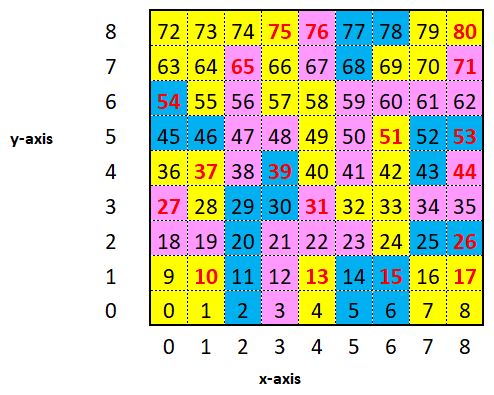
In this step we look at every one of the 65,536 possible grids (from step 1) only pick those where:
- they have a 5 and 4 in cells as per grid provided in question
- any region that consists of 2 cells only, the total adds up to 15. Example: The sum of cells 4 and 13 must be 15. Same for cell 25 and 26. This check is done in function
check54in the source code.
Going through this checks reduced the possible grid combinations from 65,536 to a manageable 416.
Step 3. Use recursive backtracking on every grid until solution found
In step 3 – I use a recursive backtracking approach and test if numbers as per rules provided can be placed in any of the 416 grids. The path or order in which the numbers were evaluated in the backtracking algorithm was from bottom left (cell 0) to top right (cell 80). A 2 dimensional array of integers was used to model the grid.
Checks that are done during the recursive backtracking process are:
- Check that total for every region adds up to 15. This check is done when the last cell of the region is reached. In image above, it is the cells marked in red – function
check_regionin code - That every 2x2 grid has at least one open space – function
is_validin code - When full board is solved, check that it is a connected region – function
is_connectedin code below
Total program runtime was ~8 seconds which is less than ~20 ms per grid evaluated.
C:\>hooks.exe
First position: "00000000"
Last position: "33333333"
Total positions: 65536
Valid positions: 416
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
..................................................
........................
Found a solution!!!!
0 0 0 8 8 0 8 8 0
0 0 0 0 7 7 7 0 0
0 0 5 0 4 0 4 0 9
8 7 5 0 3 0 4 0 9
8 0 5 3 0 2 4 6 9
8 7 0 3 1 2 0 6 0
0 7 0 0 5 0 5 6 9
8 7 0 0 6 6 0 6 0
0 0 9 9 9 0 9 9 0
..........................................
All done!
Step 4. Calculate the product of connected empty cells
With a solved grid, the final step was done manually.
(A) Remove numbers from solution above to get all the empty regions (0's)
(B) Ignore regions with only one empty space
(A) (B)
0 0 0 . . 0 . . 0 0 0 0 . . . . . 0
0 0 0 0 . . . 0 0 0 0 0 0 . . . 0 0
0 0 . 0 . 0 . 0 . 0 0 . 0 . 0 . 0 .
. . . 0 . 0 . 0 . . . . 0 . 0 . 0 .
. 0 . . 0 . . . . . . . . . . . . .
. . 0 . . . 0 . 0 ---> . . 0 . . . . . .
0 . 0 0 . 0 . . . . . 0 0 . . . . .
. . 0 0 . . 0 . 0 . . 0 0 . . . . 0
0 0 . . . 0 . . 0 0 0 . . . . . . 0
The product of the sizes of the empty spaces
= 11 * 2 * 5 * 5 * 2 * 2
= 2200
Submitted 2200, and it got my name on the leader-board!
Why use OCaml?
Any all purpose programming language can be used for this puzzle. I decided to use OCaml.
NOTE: I’m not an OCaml guru, at best I am an enthusiastic beginner. Chances are I am using it all wrong – however I was able to reach my goal - which was to solve the puzzle quickly and with lots of fun along the way.
Why use OCaml and not [insert your favourite language]?
- Speed: OCaml runtimes are fast - same order of magnitude as C++, Java, C# or F#.
- Easy to use: OCaml is a functional language but also provides great support for imperative programming, which I am more familiar with.
- A bit of variety: Knowing multiple languages widens your thought process and makes you a well-rounded developer.
- Scope: OCaml is a strong static typing language with type inference. Strongly typing results in slightly longer coding time than say Python but I found that a lot less debugging is required. With infered typing – the code is terse / not very verbose.
- Portable / Easy deploy: I initially coded and tested the program on my Windows laptop but I was also able to compile and run the final version on a Linux server.
- Jane Street is a major user of OCaml, so thought it would be a fitting tribute!
Things that can be done better
The program was cobbled together very quickly in order to solve the problem as soon as possible. Very little attention was given to have the most performant code. I did use some profiling tools after the fact to get an idea what of can be improved.
Profiling - execution count with ocamlprof
The profiling functionality is part of OCaml and records how many times functions are called, branches of conditionals are taken. It works on Windows or Linux.
c:\> ocamloptp -P a hooks7.ml -o hooks7.exe
c:\> hooks7.exe # which creates file ocamlprof.dump
c:\> ocamlprof hooks7.ml
Profiling the execution count is particularly handy to confirm that the algorithm is working as you expect.
The ocamlprof command produces a source listing of the program modules where execution counts have been inserted as comments. Below is a snippit of the profiling results. Example, the solve function was called 18_228_759 times, the is_valid function was called 32_626_539 times and only 1 is_connected grid was found.
let is_valid option_grid cell y x =
(* 32626539 *) check_region cell option_grid &&
(y = 0 || x = 0 || option_grid.(x).(y) = Some 0 ||
option_grid.(x).(y-1) = Some 0 ||
option_grid.(x-1).(y) = Some 0 || option_grid.(x-1).(y-1) = Some 0)
(* recursive backtracking function *)
let rec solve some_grid full_grid cell =
(* 18228759 *) let (x, y) = cell2xy cell in
if cell = 81 then (* 6 *) begin
if is_connected some_grid then (* 1 *) begin
print_endline "\nFound a solution!!!!";
Time Profiling
The total execution time can also be profiled. In this case, to determine how much time is spent in every function. The two main tools are gprof and perf - but gprof only works with OCaml 4.08.1 or earlier.
$ ocamlopt -p hooks7.ml -o hooks7.exe
$ ./hooks7.exe # which creates the file: gmon.out
$ gprof hooks7.exe # which displays the results
See sample output below. You can see that 41% of the time and a high number of calls, are spent in the get_population function, which is used to work out the next number to place in a hook.
Flat profile:
Each sample counts as 0.01 seconds.
% cumulative self self total
time seconds seconds calls s/call s/call name
41.31 5.92 5.92 17776970 0.00 0.00 camlHooks7__get_population_338
18.92 8.63 2.71 365735014 0.00 0.00 compare_val
5.76 9.45 0.83 69651556 0.00 0.00 camlHooks7__remove_val_245
3.74 9.99 0.54 17776970 0.00 0.00 camlHooks7__destutter_83
3.70 10.52 0.53 32626539 0.00 0.00 camlHooks7__fun_526
3.07 10.96 0.44 52304243 0.00 0.00 camlHooks7__cval_361
3.07 11.40 0.44 75544989 0.00 0.00 caml_page_table_lookup
2.93 11.82 0.42 17776974 0.00 0.00 camlHooks7__solve_371
2.86 12.23 0.41 17776968 0.00 0.00 camlStdlib__list__exists_314
2.79 12.63 0.40 32626539 0.00 0.00 camlHooks7__check_region_358
1.85 12.89 0.27 70533002 0.00 0.00 camlHooks7__cell2yx_251
...
With above profile findings, I added an inline attribute to the get_population function declaration. The total program runtime reduced from 14 seconds down to 8 seconds - a 40% improvement!
Change line from:
let get_population grid full_grid n bin =
to:
let[@inlne] get_population grid full_grid n =
Time Profiling with perf
The perf Linux utility can also be used for time profiling - the results looks very similar to that of gprof. It is not as easy to use as gprof but at least it works with latest version of OCaml. It does not work on Windows.
$ ocamlopt -g hooks7.ml -o hooks7.exe
$ perf record --call-graph=dwarf -- ./hooks7.exe
$ perf report
OCaml source code
(*
* Jane Street Puzzle - Feb 2021
* Willem Hoek <willem@matimba.com>
* Blog Post: https://whoek.com/b/janestreet-puzzle-feb-2021-solved-ocaml-to-the-rescue
*)
(**** START of HELPER functions *************************************)
(* option_to_int : option int -> int *)
let option_to_int = function
| Some x -> x
| None -> 0
(* remove consecutive duplicates from a list *)
(* https://dev.realworldocaml.org/lists-and-patterns.html#scrollNav-6-1 *)
let rec destutter = function
| [] | [_] as l -> l
| hd :: (hd' :: _ as tl) when hd = hd' -> destutter tl
| hd :: tl -> hd :: destutter tl
(* print matrix : int array array -> unit *)
let print_matrix matrix =
let dimx = Array.length matrix in
let dimy = Array.length matrix.(0) in
for x = 0 to (dimx - 1) do
for y = (dimy - 1) downto 0 do
Printf.printf "%i " matrix.(x).(y);
done;
Printf.printf "\n%!"
done;
Printf.printf "\n%!"
(* convert matrix : option int array array -> int array array *)
let int_of_matrix matrix =
let dimx = Array.length matrix in
let dimy = Array.length matrix.(0) in
let m = Array.make_matrix dimx dimy 0 in
for x = 0 to (dimx - 1) do
for y = 0 to (dimy - 1) do
m.(x).(y) <- option_to_int matrix.(x).(y)
done
done;
m
(* get last element in a list *)
let rec list_last = function
| [] -> failwith "List is empty"
| [x] -> x
| hd :: tl -> list_last tl
(* math power function *)
let rec power x y =
if(y <= 1 ) then x else x * power x (y-1)
(* convert from base 10 to base n where n < 10 : int -> int -> string *)
let rec frombase10 x n =
let digit = x mod n in
let div = x / n in
if div = 0 then string_of_int digit
else (frombase10 div n) ^ string_of_int digit
(* return right n characters of as string : string -> int -> string *)
let right_str str n =
let len = String.length str in
String.sub str (len - n) n
(* remove first item with value v from a list *)
let rec remove_val v = function
| [] -> []
| h :: t -> if h = v then t else h :: remove_val v t
(**** END of HELPER functions ***************************************)
(* convert from cell number to x y coordinate of 9x9 grid *)
let cell2xy cell =
let y = cell / 9 in
let x = cell mod 9 in
(x, y)
let prefix_zeros x = right_str ("00000000" ^ x) 8
(* TEST prefix_zeros *)
let () = assert ("00001111" = prefix_zeros "1111")
(* create list of all the possible hook alignments *)
let make_list first last = (* n = size of the grid *)
let base4 x = prefix_zeros @@ frombase10 (x + first) 4 in
List.init (last - first) base4
(* add one hook to grid where corner is at coordinate provided *)
let fill_hook grid num (x, y) =
for i = 0 to 8 do
if grid.(i).(y) = 1 then grid.(i).(y) <- num;
if grid.(x).(i) = 1 then grid.(x).(i) <- num
done;
grid
(* create grid with all the hooks filled in *)
(* string -> int array array *)
let place_hooks str =
let grid = ref (Array.make_matrix 9 9 1) in (* x y default_value *)
let y_bottom = ref 0 in
let y_top = ref 8 in
let x_left = ref 0 in
let x_right = ref 8 in
let rec add_hook sub_str =
let len = String.length sub_str in
if len = 0 then !grid
else begin
match sub_str.[0] with
| '0' -> grid := fill_hook !grid (len + 1) (!x_left, !y_bottom);
y_bottom := !y_bottom + 1;
x_left := !x_left + 1;
add_hook (right_str sub_str (len - 1))
| '1' -> grid := fill_hook !grid (len + 1) (!x_left, !y_top);
y_top := !y_top - 1;
x_left := !x_left + 1;
add_hook (right_str sub_str (len - 1))
| '2' -> grid := fill_hook !grid (len + 1) (!x_right, !y_top);
y_top := !y_top - 1;
x_right := !x_right - 1;
add_hook (right_str sub_str (len - 1))
| '3' -> grid := fill_hook !grid (len + 1) (!x_right, !y_bottom);
y_bottom := !y_bottom + 1;
x_right := !x_right - 1;
add_hook (right_str sub_str (len - 1))
| _ -> assert false
end
in add_hook str
(* basic checks being done to get a subset of grids *)
let check54 grid =
grid.(4).(0) + grid.(4).(1) = 15
&& grid.(4).(7) + grid.(4).(8) = 15
&& grid.(7).(2) + grid.(8).(2) = 15
&& grid.(4).(2) = 5
&& grid.(4).(6) = 4
(* All possible entries for full grid *)
let bin = [|[];[1];[2;2;0];[3;3;3;0;0];[4;4;4;4;0;0;0];[5;5;5;5;5;0;0;0;0];
[6;6;6;6;6;6;0;0;0;0;0];[7;7;7;7;7;7;7;0;0;0;0;0;0];
[8;8;8;8;8;8;8;8;0;0;0;0;0;0;0];[9;9;9;9;9;9;9;9;9;0;0;0;0;0;0;0;0]|]
(* get list of possible remaining values to place in a hook *)
let[@inlne] get_population grid full_grid n =
let p = ref bin.(n) in
for x = 0 to 8 do
for y = 0 to 8 do
if full_grid.(x).(y) = n && grid.(x).(y) <> None
then begin
let to_remove = option_to_int @@ grid.(x).(y) in
p := remove_val to_remove !p
end
done
done;
destutter @@ !p (* to remove duplucates *)
(* TEST get_population *)
let () =
let grid = Array.make_matrix 9 9 (Some 9) in
let full_grid = Array.make_matrix 9 9 1 in
full_grid.(1).(1) <- 3;
full_grid.(2).(1) <- 3;
full_grid.(3).(1) <- 3;
full_grid.(4).(1) <- 3;
grid.(1).(1) <- None;
grid.(2).(1) <- Some 3;
grid.(3).(1) <- Some 0;
grid.(4).(1) <- Some 0;
assert ([3] = get_population grid full_grid 3);
assert ([4; 0] = get_population grid full_grid 4)
(* test that the final solution consists of connected values *)
let is_connected some_grid =
let mark = Array.make_matrix 9 9 true in
let count = ref 0 in
let rec flood x y =
incr count;
mark.(x).(y) <- false;
if y > 0 && option_to_int @@ some_grid.(x).(y-1) <> 0 && (* N *)
mark.(x).(y-1) then flood x (y-1);
if y < 8 && option_to_int @@ some_grid.(x).(y+1) <> 0 && (* S *)
mark.(x).(y+1) then flood x (y+1);
if x > 0 && option_to_int @@ some_grid.(x-1).(y) <> 0 && (* W *)
mark.(x-1).(y) then flood (x-1) y;
if x < 8 && option_to_int @@ some_grid.(x+1).(y) <> 0 && (* E *)
mark.(x+1).(y) then flood (x+1) y;
in
let () = flood 4 2 in (* starting point - known number in grid *)
!count = 45 (* 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 *)
(* sum of every region must add up to 15 *)
let check_region region option_grid =
let cval cell =
let x,y = cell2xy cell in
option_to_int option_grid.(x).(y)
in
match region with
| 10 -> 15 = cval 0 + cval 1 + cval 9 + cval 10
| 13 -> 15 = cval 4 + cval 13
| 15 -> 15 = cval 5 + cval 6 + cval 14 + cval 15
| 17 -> 15 = cval 7 + cval 8 + cval 16 + cval 17
| 26 -> 15 = cval 25 + cval 26
| 27 -> 15 = cval 18 + cval 19 + cval 27
| 31 -> 15 = cval 3 + cval 12 + cval 21 + cval 22 + cval 23 + cval 31
| 37 -> 15 = cval 28 + cval 36 + cval 37
| 39 -> 15 = cval 2 + cval 11 + cval 20 + cval 29 + cval 30 + cval 39
| 44 -> 15 = cval 34 + cval 35 + cval 44
| 51 -> 15 = cval 24 + cval 32 + cval 33 + cval 42 + cval 51
| 53 -> 15 = cval 43 + cval 52 + cval 53
| 54 -> 15 = cval 45 + cval 46 + cval 54
| 65 -> 15 = cval 38 + cval 47 + cval 48 + cval 56 + cval 65
| 71 -> 15 = cval 41 + cval 50 + cval 59 + cval 60 + cval 61 + cval 62 + cval 71
| 75 -> 15 = cval 40 + cval 49 + cval 55 + cval 57 + cval 58 + cval 63 + cval 64
+ cval 66 + cval 72 + cval 73 + cval 74 + cval 75
| 76 -> 15 = cval 67 + cval 76
| 78 -> 15 = cval 68 + cval 77 + cval 78
| 80 -> 15 = cval 69 + cval 70 + cval 79 + cval 80
| _ -> true
(* every 2x2 region must have at least one empty cell *)
let is_valid option_grid cell x y =
check_region cell option_grid
&& (y = 0 || x = 0
|| option_grid.(x).(y) = Some 0
|| option_grid.(x).(y-1) = Some 0
|| option_grid.(x-1).(y) = Some 0
|| option_grid.(x-1).(y-1) = Some 0)
(* recursive backtracking - cell 0 to 80 *)
let rec solve some_grid full_grid cell =
let (x, y) = cell2xy cell in
if cell > 80 then begin
if is_connected some_grid then begin
print_endline "\nFound a solution!!!!";
some_grid
|> int_of_matrix
|> print_matrix;
true
end
else false
end
else if some_grid.(x).(y) <> None then solve some_grid full_grid (cell + 1)
else
let hook_num = full_grid.(x).(y) in
let population = get_population some_grid full_grid hook_num in
let check p =
some_grid.(x).(y) <- Some p;
if is_valid some_grid cell x y &&
solve some_grid full_grid (cell + 1)
then true
else (
some_grid.(x).(y) <- None;
false
)
in
List.exists check population
let main () = begin
let all_hooks = make_list 0 (power 4 8) in (*65_536 *)
let valid_hooks = List.filter (fun x -> check54 @@ place_hooks x) all_hooks in
Printf.printf "First position: %S\n" (List.hd all_hooks);
Printf.printf "Last position: %S\n" (list_last all_hooks);
Printf.printf "Total positions: %i\n" (List.length all_hooks);
Printf.printf "Valid positions: %i\n" (List.length valid_hooks);
let solve_grid hooks =
let empty_grid = (Array.make_matrix 9 9 None) in
empty_grid.(4).(2) <- Some 5;
empty_grid.(4).(6) <- Some 4;
let full_grid = place_hooks hooks in
let _ = solve empty_grid full_grid 0 in
Printf.printf ".%!";
in
List.iter solve_grid valid_hooks;
print_endline "\nAll done!"
end;;
main ()
Development environment
Development and testing:
- Operating System, Windows 10
- OCaml for Windows version 4.11.1 using the 64-bit Graphical Installer
- Editor: Emacs for Cygwin, with Tuareg
- For time profiling, I use a Debian 10 VPS hosted at Linode
- I have been unable to get merlin working with above setup – anyone who is using Emacs for Cygwin with merlin, please let me know the secret.
Testing during development is mostly done via utop.
c:\> utop
utop # #use "hooks7.ml";;
Compile and run
c:\> ocamloptp hooks7.ml -o hooks7.exe -unsafe -rectypes -inline 1000 -O3
c:\> hooks7.exe
Thank you to Jane Street for publishing the puzzle. If you found this post of use or have any comments, please let me know. My email is in the source code.
References and further reading
[1] Jane Street - Puzzle Archive.
https://www.janestreet.com/puzzles/hooks-7/. Retrieved: 2021-01-05
[2] Source code for this post on Github.
https://github.com/whoek/janestreet-puzzles/tree/master/2021-02. Retrieved: 2021-03-08
[3] Lecture 15 - Backtracking by Steven Skiena
https://www3.cs.stonybrook.edu/~algorith/video-lectures/2007/lecture15.pdf Retrieved: 2020-01-05
[4] OCaml programming language.
https://ocaml.org/. Retrieved: 2020-01-05
[5] A Taste of OCaml’s Predictable Performance
https://devpoga.org/post/2020-11-21-a-taste-of-ocaml-predictable-performance/ Retrieved: 2020-02-14
Similar Posts on this website
How-to Import an Excel file into SQLite and back to Excel again
Solving the Jane Street puzzle of December 2022
Why I created Scrumdog - a program to download Jira Issues to a local database
Solving the Jane Street puzzle of Dec 2020 - Backtracking with OCaml
Automate your Jira reporting with Python and Excel