Willem Hoek
Solving the Jane Street puzzle of December 2022
Jan 02, 2023
Die Agony
This post describes the approach and solution to the Jane Street Puzzle of December 2022.
Approach
I solved it programmatically using a recursive backtracking algorithm, which works very well for these type of problems. Backtracking is where you incrementally try different paths and abondon a candidate (“backtrack”) as soon as a path is not valid any more.
The provided grid of 36 cells were numbered from 0 to 35 which represent the nodes in the search tree.
30 31 32 33 34 35
24 25 26 27 28 29
18 19 20 21 22 23
12 13 14 15 16 17
6 7 8 9 10 11
0 1 2 3 4 5
The recursive function named solve starts at cell 0 and meanders the grid until it gets to cell 35.
The puzzle stated that we have a “six-sided die, with numbers”. Although with a standard die - the numbers are integers, I decided not to assume this. Hence I used floats in the grid array to store the values. As it turns out – they were all integers.
When you run the program, it should show all the paths evaluated and the solution.
final path = 0 6 7 8 2 1 7 13 19 25 31 32 26 25 24 18 19 20 14 15 9 3 4 5 11 17 16 15 21 27 28 29 35
dice = top:7 bottom:9 up:5 down:-9 left:9 right:-3
unvisited cells = 34 33 30 23 22 12 10
Sum of values in the unvisited cells = 1935
Here is a visual showing the backtracking in action and related Python code to generate the image.
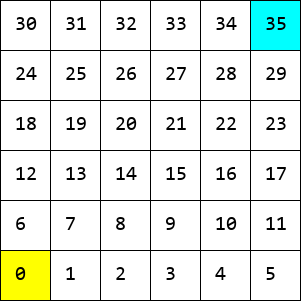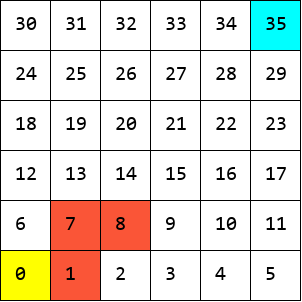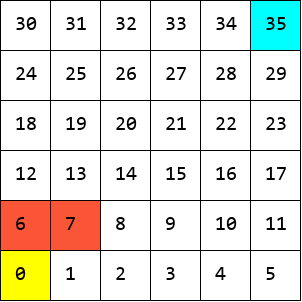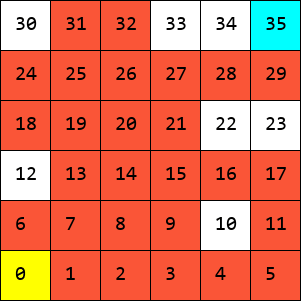
Using OCaml
Since Jane Street is a major user of OCaml, I decided to use OCaml for this puzzle.
The code, listed below, is quite short. Less than half the code solve the actual puzzle. The rest of the code is used to print out the evaluated paths and solution. The evaluated paths from the output was used to generate the pretty backtracking image above – using Python Pillow library.
The good news is – you do not need OCaml installed on your computer to run the code below. There are multiple FREE online OCaml Compilers available on the web. Below is a list of some of them.
- https://www.jdoodle.com/compile-ocaml-online/
- https://www.onlinegdb.com/online_ocaml_compiler
- https://sketch.sh/new/ocaml
- https://try.ocamlpro.com/
- https://ocaml.godbolt.org/
Simply copy / paste the source code below into the online OCaml Compiler and execute to see the results.
(*********************************
Author: Willem Hoek
Date: 26 Dec 2022
Website: whoek.com
**********************************)
type move = Up | Down | Left | Right
let roll_dice (top, bottom, up, down, left, right) d =
match d with
| Up -> down, up, top, bottom, left, right
| Down -> up, down, bottom, top, left, right
| Right -> left, right, up, down, bottom, top
| Left -> right, left, up, down, top, bottom
let next_cell cell move =
match move with
| Up -> cell + 6
| Down -> cell - 6
| Left -> cell - 1
| Right -> cell + 1
let valid_moves cell =
(
match cell with
| 0 | 6 | 12 | 18 | 24 | 30 -> [Right]
| 5 | 11 | 17 | 23 | 29 | 35 -> [Left]
| _ -> [Right; Left]
) @ (
match cell with
| 0 | 1 | 2 | 3 | 4 | 5 -> [Up]
| 30 | 31 | 32 | 33 | 34 | 35 -> [Down]
| _ -> [Up; Down]
)
let grid =
[|
0. ; 77.; 32.; 403.; 337.; 452.;
5. ; 23.; -4.; 592.; 445.; 620.;
-7. ; 2.; 357.; 452.; 317.; 395.;
186.; 42.; 195.; 704.; 452.; 228.;
81. ; 123.; 240.; 443.; 353.; 508.;
57. ; 33.; 132.; 268.; 492.; 732.;
|]
let print_dice dice =
let a, b, c, d, e, f = dice in
Printf.printf "dice = top:%g bottom:%g up:%g down:%g left:%g right:%g\n"
a b c d e f
let print_int_lst p =
List.iter (Printf.printf "%i ") p;
Printf.printf "\n"
let unvisited all visited =
List.filter (fun x -> not @@ List.mem x visited) all
let () = assert (unvisited [1;2;3;4] [1;3] = [2;4])
let sum_values lst =
let f acc cell = acc +. grid.(cell) in
List.fold_left f 0.0 lst
let () = assert (sum_values [6; 35] = 737.0)
let range i = List.init i succ
let () = assert (range 3 = [1; 2; 3])
let print_solution ~new_dice ~cell ~path =
let all = range 35 in
let unvisited_cells = unvisited all @@ cell :: path in
let sum_of_values = sum_values unvisited_cells in
print_dice new_dice;
Printf.printf "unvisited cells = ";
print_int_lst unvisited_cells;
Printf.printf "Sum of values in the unvisited cells = %g\n"
sum_of_values
let rec solve ~dice ~cell ~n ~path ~score =
print_int_lst @@ List.rev @@ cell :: path;
let new_score = grid.(cell) in
let new_top = (
if n = 0.0 then 0.
else (new_score -. score) /. n
) in
let top, d2, d3, d4, d5, d6 = dice in
let new_dice = new_top, d2, d3, d4, d5, d6 in
let valid = (top = new_top || top = 0.) in
if cell = 35 && valid then begin
Printf.printf "Solution found!!!\n";
print_solution ~new_dice ~cell ~path;
true (* stop looking *)
end
else if valid then begin
let moves = valid_moves cell in
let check move =
let new_cell = next_cell cell move in
solve ~dice:(roll_dice new_dice move)
~cell:new_cell
~n:(n +. 1.)
~path:(cell :: path)
~score:new_score
in
List.exists check moves
end
else false (* backtrack *)
let main () =
let dice = 0.0, 0.0, 0.0, 0.0, 0.0, 0.0 in
let _ = solve ~dice ~cell:0 ~n:0.0 ~path:[] ~score:0.0 in
Printf.printf "Cheers!\n"
let () = main ()
References and further reading
[1] Jane Street - Puzzle Archive
https://www.janestreet.com/puzzles/archive/
[2] Source code for this post on Github
https://github.com/whoek/janestreet-puzzles
[3] OCaml programming language
https://ocaml.org/
[4] Backtracking Algorithm
https://en.wikipedia.org/wiki/Backtracking
[5] Solving a previous Jane Street puzzle – also using recursive backtracking and Ocaml
https://whoek.com/b/janestreet-puzzle-feb-2021-solved-ocaml-to-the-rescue
[6] OCaml Tips: Implementing a range Function
https://batsov.com/articles/2022/10/31/ocaml-tips-implementing-a-range-function/
Similar Posts on this website
How-to Import an Excel file into SQLite and back to Excel again
Why I created Scrumdog - a program to download Jira Issues to a local database
Jane Street puzzle Feb 2021 SOLVED! OCaml to the rescue
Solving the Jane Street puzzle of Dec 2020 - Backtracking with OCaml
Automate your Jira reporting with Python and Excel