Willem Hoek
Solving the Jane Street puzzle of Dec 2020 - Backtracking with OCaml
Jan 10, 2021

Nighthawks, Edward Hopper, 1942
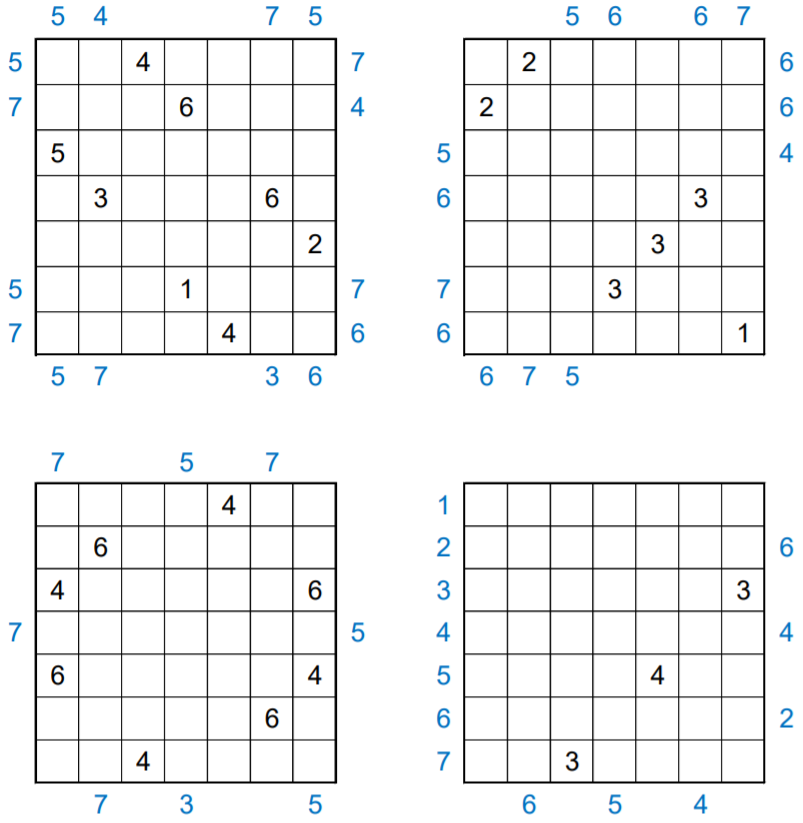
Twenty Four Seven 2-by-2 #2
Every month Jane Street Capital publishes a puzzle on their website. This was the puzzle and solution for December 2020 [1].
Each of the grids below is incomplete. Place numbers in some of the empty cells so that in total each grid’s interior contains one 1, two 2’s, etc., up to seven 7’s. Furthermore, each row and column within each grid must contain exactly 4 numbers which sum to 20. Finally, the numbered cells must form a connected region, but every 2-by-2 subsquare in the completed grid must contain at least one empty cell.
Some numbers have been placed inside each grid. Additionally, some blue numbers have been placed outside of the grids. These blue numbers indicate the first value seen in the corresponding row or column when looking into the grid from that location.
Once each of the grids is complete, create a 7-by-7 grid by “adding” the four grids’ interiors together (as if they were 7-by-7 matrices). The answer to this month’s puzzle is the sum of the squares of the values in this final grid.
Approach followed
I started to solve it with pen and paper but realised it will take way to long - probably quicker to do it programmatically. The puzzles look like a Suduko puzzle. Backtracking [3] is one of the widely used methods to solve Soduko – so I decided to use that.
Pseudo code for recursive backtracking function – this is the solve function in code below.
function: solve (grid, node)
if at a solution – return success (true)
else for every possible choice at node
if valid choice then solve for next step along path
if successful return success (true)
else restore the state as at beginning of loop
If no solution, report failure (false)
Solution
Puzzle 1 -- 2 seconds
5 4 4 0 0 7 0
0 0 7 6 3 4 0
5 6 2 0 7 0 0
0 3 0 0 6 6 5
5 7 0 6 0 0 2
5 0 7 1 0 0 7
0 0 0 7 4 3 6
Puzzle 2 -- 971 seconds
7 2 5 6 0 0 0
2 0 0 5 7 6 0
5 7 4 0 0 4 0
0 0 6 0 4 3 7
6 4 0 0 3 0 7
0 7 5 3 0 0 5
0 0 0 6 6 7 1
Puzzle 3 -- 3248 seconds
7 2 0 0 4 7 0
0 6 7 5 2 0 0
4 5 0 5 0 0 6
0 0 0 7 7 1 5
6 7 3 0 0 0 4
3 0 6 0 0 6 5
0 0 4 3 7 6 0
Puzzle 4 -- 2923 seconds
0 0 0 1 5 7 7
0 2 5 7 0 0 6
3 7 0 7 0 0 3
4 0 0 0 5 7 4
0 5 6 5 4 0 0
6 0 6 0 6 2 0
7 6 3 0 0 4 0
Final answer = Sum of four matrices |> sum of squares = 8520
Why use OCaml and not Python?
I use Python for my day-to-day automation tasks but decided to use OCaml [4] for this exercise.
Main reasons:
- Speed: Python is slow. OCaml runtimes can easily be 50-100x faster than Python. Since I was doing this very quickly and using a brute force method, I knew that runtime might be an issue.
- Easy to use: OCaml is a functional language but also provides great support for imperative programming which is closer to Python
- Variety: Knowing multiple languages widens your thought process and makes you a well-rounded developer
Also:
- Scope: Python is dynamically scoped. OCaml is strong static typing with type inference. This results in slightly longer coding time than in Python but I found that a lot less debugging was required
- Portable / Easy deploy: I developed, compiled and tested the program on my Windows laptop and was able recompile and execute the final version on a Linux server. Similar to Python it works well on Linux, Windows and other platforms
If you are not familiar with OCaml - you may want to have look at this great talk by Yaron Minsky of Jane Street.
What can be done better?
The program was cobbled together very quickly to solve the problem ASAP. The code and patterns used were not elegant, example:
- I did not try to prune branches (remove values) when doing the backtracking - hence the fairly long runtimes
- The path (nodes) followed in grid was manually selected, it should be done programmatically to ensure most constrainted options are explored first
- The selection of possible entries for a particular node does not take into account other entries in row/column
- No benchmarking or profiling was done to speed up the code
- Better data structures can be used, I don’t think using records was a good choice to define the input data
- Did not follow DRY (“do not repeat yourself”) principles, e.g. the
check_top,check_bottom,check_left,check_rightfunctions should have been combined in one function
(***************** START helper functions *************************)
(* Convert Option to Integer. Default is 0 *)
(* https://github.com/ocaml/ocaml/blob/trunk/stdlib/option.ml *)
let oval = function
| Some x -> x
| None -> 0
(* print contents of matrix - 2-dim Array *)
let print_matrix matrix =
let dimy = Array.length matrix in
let dimx = Array.length matrix.(0) in
Printf.printf "\n%!";
for y = 0 to (dimy - 1) do
for x = 0 to (dimx - 1) do
let z = oval matrix.(y).(x) in
Printf.printf "%i " z
done;
Printf.printf "\n%!"
done;
Printf.printf "\n%!"
(* make a copy of a int array array - 2-dim Array *)
let copy_matrix matrix =
let dimy = Array.length matrix in
let dimx = Array.length matrix.(0) in
let m = Array.make_matrix dimy dimx 0 in
for y = 0 to (dimy - 1) do
for x = 0 to (dimx - 1) do
m.(y).(x) <- matrix.(y).(x)
done
done;
m
(* remove consecutive duplicates from a list *)
(* https://dev.realworldocaml.org/lists-and-patterns.html#scrollNav-6-1 *)
let rec destutter = function
| [] | [_] as l -> l
| hd :: (hd' :: _ as tl) when hd = hd' -> destutter tl
| hd :: tl -> hd :: destutter tl
(* remove nth item from a list *)
let rec remove_at n = function
| [] -> []
| h :: t -> if n = 0 then t else h :: remove_at (n-1) t
(* remove first item with value v from a list *)
let rec remove_val v = function
| [] -> []
| h :: t -> if h = v then t else h :: remove_val v t
(* convert matrix containing numbers to Some numbers and 0 is None *)
let some_of_matrix matrix =
let dimy = Array.length matrix in
let dimx = Array.length matrix.(0) in
let m = Array.make_matrix dimy dimx None in
for y = 0 to (dimy - 1) do
for x = 0 to (dimx - 1) do
let z = matrix.(y).(x) in
if z <> 0 then m.(y).(x) <- Some z
done
done;
m
(***************** END helper functions *************************)
type puzzle = {
left: int array;
right: int array;
bottom: int array;
top: int array;
grid: int array array;
path: int array;
valid_x: int; (* A cell with a known value -- starting point *)
valid_y: int; (* to check for connected region *)
}
(* list of all values that will be used in a grid *)
let population = [1;2;2;3;3;3;4;4;4;4;5;5;5;5;5;6;6;6;6;6;6;7;7;7;7;7;7;7;
0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0;0]
let cell2xy cell =
let y = cell / 7 in
let x = cell mod 7 in
(y, x)
(* not more than 4 numbers in row and column and max 20 *)
let max4 grid y x =
let y_sum = ref 0 in
let x_sum = ref 0 in
let y_count = ref 0 in
let x_count = ref 0 in
for i = 0 to 6 do
let yval = oval grid.(i).(x) in
if yval <> 0 then begin
incr y_count;
y_sum := !y_sum + yval
end;
let xval = oval grid.(y).(i) in
if xval <> 0 then begin
incr x_count;
x_sum := !x_sum + xval
end
done;
((!y_count < 4 && !y_sum < 20) || (!y_count = 4 && !y_sum = 20)) &&
((!x_count < 4 && !x_sum < 20) || (!x_count = 4 && !x_sum = 20))
let check_left p grid y x =
let v = p.left.(y) in
if v = 0 then true
else let rec check i =
match i = x, grid.(y).(i) with
| true, g when g = Some v || g = Some 0 -> true
| false, g when g = Some 0 -> check (i + 1)
| false, g when g = Some v || g = None -> true
| _, _ -> false
in check 0
let check_right p grid y x =
let v = p.right.(y) in
if v = 0 then true
else let rec check i =
match i = x, grid.(y).(i) with
| true, g when g = Some v || g = Some 0 -> true
| false, g when g = Some 0 -> check (i - 1)
| false, g when g = Some v || g = None -> true
| _, _ -> false
in check 6
let check_top p grid y x =
let v = p.top.(x) in
if v = 0 then true
else let rec check i =
match i = y, grid.(i).(x) with
| true, g when g = Some v || g = Some 0 -> true
| false, g when g = Some 0 -> check (i + 1)
| false, g when g = Some v || g = None -> true
| _, _ -> false
in check 0
let check_bottom p grid y x =
let v = p.bottom.(x) in
if v = 0 then true
else let rec check i =
match i = y, grid.(i).(x) with
| true, g when g = Some v || g = Some 0 -> true
| false, g when g = Some 0 -> check (i - 1)
| false, g when g = Some v || g = None -> true
| _, _ -> false
in check 6
(* check that at least one blank cell in a 2x2 sub matrix *)
let one_zero grid y x =
if grid.(y).(x) = Some 0 || y = 0 || x = 0 || y = 6 || x = 6 then true
else
let e = grid.(y).(x+1) in
let w = grid.(y).(x-1) in
let n = grid.(y-1).(x) in
let s = grid.(y+1).(x) in
let ne = grid.(y-1).(x+1) in
let se = grid.(y+1).(x+1) in
let nw = grid.(y-1).(x-1) in
let sw = grid.(y+1).(x-1) in
(e = None || e = Some 0 || n = None || n = Some 0 || ne = None || ne = Some 0) &&
(e = None || e = Some 0 || s = None || s = Some 0 || se = None || se = Some 0) &&
(w = None || w = Some 0 || n = None || n = Some 0 || nw = None || nw = Some 0) &&
(w = None || w = Some 0 || s = None || s = Some 0 || sw = None || sw = Some 0)
let connected grid y x =
let () = assert (grid.(y).(x) <> Some 0) in
let mark = Array.make_matrix 7 7 true in
let count = ref 0 in
let rec flood y x =
incr count;
mark.(y).(x) <- false;
if y > 0 && grid.(y-1).(x) <> Some 0 && mark.(y-1).(x) then flood (y-1) x; (* N *)
if y < 6 && grid.(y+1).(x) <> Some 0 && mark.(y+1).(x) then flood (y+1) x; (* S *)
if x > 0 && grid.(y).(x-1) <> Some 0 && mark.(y).(x-1) then flood y (x-1); (* W *)
if x < 6 && grid.(y).(x+1) <> Some 0 && mark.(y).(x+1) then flood y (x+1); (* E *)
in
let () = flood y x in
!count >= 28 (* 28 if all items on board - else more*)
let isvalid p grid step cell y x =
max4 grid y x &&
check_left p grid y x &&
check_right p grid y x &&
check_top p grid y x &&
check_bottom p grid y x &&
one_zero grid y x &&
connected grid p.valid_y p.valid_x
(* remove already used numbers from full population *)
let get_population grid =
let p = ref population in
for i = 0 to 6 do
for j = 0 to 6 do
if grid.(i).(j) <> None then
p := remove_val (Option.get grid.(i).(j)) !p;
done
done;
!p
(* recursive backtracking function *)
let rec solve p grid step =
let cell = p.path.(step) in
let (y, x) = cell2xy cell in
let getpop = get_population grid in
let pop = getpop |> destutter in
let length_pop = List.length pop - 1 in
try
if getpop = [] then begin
print_endline "\n...solved!!";
true
end
else begin
for n = 0 to length_pop do
let v = List.nth pop n in
grid.(y).(x) <- Some v;
if isvalid p grid step cell y x then begin
if solve p grid (step + 1) then begin
raise Exit
end
end;
grid.(y).(x) <- None
done;
false
end
with Exit -> true
(******************* SOLVE ********************************************)
let p1 = {left = [|5; 7; 0; 0; 0; 5; 7|];
right = [|7; 4; 0; 0; 0; 7; 6|];
top = [|5; 4; 0; 0; 0; 7; 5|];
bottom = [|5; 7; 0; 0; 0; 3; 6|];
grid = [|[|0;0;4;0;0;0;0|];
[|0;0;0;6;0;0;0|];
[|5;0;0;0;0;0;0|];
[|0;3;0;0;0;6;0|];
[|0;0;0;0;0;0;2|];
[|0;0;0;1;0;0;0|];
[|0;0;0;0;4;0;0|]|];
path = [|0;42;48;6;1;7;35;43;47;41;13;5;8;15;9;12;
19;11;36;29;37;40;33;39;28;21;4;3;20;27;44;45;16;
23;30;18;25;32;17;24;31;
0|];
valid_y = 0;
valid_x = 2;
}
let p2 = {left = [|0; 0; 5; 6; 0; 7; 6|];
right = [|6; 6; 4; 0; 0; 0; 0|];
top = [|0; 0; 5; 6; 0; 6; 7|];
bottom = [|6; 7; 5; 0; 0; 0; 0|];
grid = [|[|0;2;0;0;0;0;0|];
[|2;0;0;0;0;0;0|];
[|0;0;0;0;0;0;0|];
[|0;0;0;0;0;3;0|];
[|0;0;0;0;3;0;0|];
[|0;0;0;3;0;0;0|];
[|0;0;0;0;0;0;1|]|];
path = [|42;6;35;43;44;13;20;5;14;21;2;3;41;47;36;37;19;12;9;10;
15;22;40;4;11;18;39;45;46;16;23;30;17;24;31;25;27;34;28;29;8;33;0;
0|];
valid_y = 0;
valid_x = 1;
}
let p3 = {left = [|0; 0; 0; 7; 0; 0; 0|];
right = [|0; 0; 0; 5; 0; 0; 0|];
top = [|7; 0; 0; 5; 0; 7; 0|];
bottom = [|0; 7; 0; 3; 0; 0; 5|];
grid = [|[|0;0;0;0;4;0;0|];
[|0;6;0;0;0;0;0|];
[|4;0;0;0;0;0;6|];
[|0;0;0;0;0;0;0|];
[|6;0;0;0;0;0;4|];
[|0;0;0;0;0;6;0|];
[|0;0;4;0;0;0;0|]|];
path = [|0;7;21;22;23;24;25;26;27;43;36;29;15;3;45;10;38;31;17;
5;12;19;33;48;41;9;11;18;16;30;32;35;37;39;42;46;47;1;2;6;13;
0|];
valid_y = 0;
valid_x = 4;
}
let p4 = {left = [|1; 2; 3; 4; 5; 6; 7|];
right = [|0; 6; 0; 4; 0; 2; 0|];
top = [|0; 0; 0; 0; 0; 0; 0|];
bottom = [|0; 6; 0; 5; 0; 4; 0|];
grid = [|[|0;0;0;0;0;0;0|];
[|0;0;0;0;0;0;0|];
[|0;0;0;0;0;0;3|];
[|0;0;0;0;0;0;0|];
[|0;0;0;0;4;0;0|];
[|0;0;0;0;0;0;0|];
[|0;0;3;0;0;0;0|]|];
path = [|42;35;28;21;14;7;0;43;45;47;41;27;13;36;29;22;15;8;1;40;33;26;19;12;
5;37;39;38;30;31;23;25;24;9;10;11;17;3;16;18;2;4;6;34;46;48;
0|];
valid_y = 6;
valid_x = 2;
}
let () =
print_endline "Puzzle 1";
let t = Sys.time() in
let g1 = copy_matrix p1.grid |> some_of_matrix in
let _ = solve p1 g1 0 in
print_matrix g1;
Printf.printf "Execution time: %fs\n" (Sys.time() -. t)
let () =
print_endline "Puzzle 2";
let t = Sys.time() in
let g2 = copy_matrix p2.grid |> some_of_matrix in
let _ = solve p2 g2 0 in
print_matrix g2;
Printf.printf "Execution time: %fs\n" (Sys.time() -. t)
let () =
print_endline "Puzzle 3";
let t = Sys.time() in
let g3 = copy_matrix p3.grid |> some_of_matrix in
let _ = solve p3 g3 0 in
print_matrix g3;
Printf.printf "Execution time: %fs\n" (Sys.time() -. t)
let () =
print_endline "Puzzle 4";
let t = Sys.time() in
let g4 = copy_matrix p4.grid |> some_of_matrix in
let _ = solve p4 g4 0 in
print_matrix g4;
Printf.printf "Execution time: %fs\n" (Sys.time() -. t)
References and further reading
[1] Jane Street - Puzzle Archive.
https://www.janestreet.com/puzzles/twenty-four-seven-2-by-2-2/. Retrieved: 2021-01-05
[2] Source code for this post on Github.
https://github.com/whoek/janestreet-puzzles/tree/master/2020-12. Retrieved: 2020-01-05
[3] Lecture 15 - Backtracking by Steven Skiena
https://www3.cs.stonybrook.edu/~algorith/video-lectures/2007/lecture15.pdf Retrieved: 2020-01-05
[4] OCaml programming language.
https://ocaml.org/. Retrieved: 2020-01-05
Similar Posts on this website
How-to Import an Excel file into SQLite and back to Excel again
Solving the Jane Street puzzle of December 2022
Why I created Scrumdog - a program to download Jira Issues to a local database
Jane Street puzzle Feb 2021 SOLVED! OCaml to the rescue
Automate your Jira reporting with Python and Excel